Every industrial hyperspectral detector on the market can distinguish between an apple and a tomato due to their different spectral signatures, and the typically large number of pixels available on each object. Will this still be the case if the apple and the tomato were only a few pixels large?
The keystone specification of any hyperspectral system is one of the most important parameters defining its usability. However, it is also the most overlooked parameter during the selection phase. Keystone introduces a spatial misregistration problem between the spectral bands. It means that the spectral information in an image pixel is made up by parts of the spectra from different spatial positions on the scene around that pixel. In essence, a keystone in the data will generate unphysical spectra that do not correspond to the objects in the image.
Evaluating the performance of a hyperspectral camera based only on the nominal specifications can be very hard. It is common to encounter misleading keystone values and it is not uncommon to find values for keystone in datasheets defined simply as “low” or “negligible”, either. This hardly provides useful information by itself, so it is preferred to define it as a percentage of the pixel size e.g. 10% of a pixel (or supply a keystone map of the whole sensor). Some, of the many different suppliers of hyperspectral cameras, offer solutions with nominal keystone values in the range of 10% to 75% of the pixel size (some even try to make it look smaller by defining it as e.g. ±35%), and even higher values for less robust systems.
Suppose that a pushbroom-scanning hyperspectral camera is being used, with e.g. 1240 nominal pixels specified in the datasheet and that the keystone in the system is, misleadingly, simply defined as “low”. Without further information, the ability to record up to 1240 unique and correct spectral signatures per scanned spatial line, thus reproducing the real radiance from each pixel in the scene, should be expected. Further assume that there are two objects in the scene, positioned next to each other and that these objects are spectrally different. Should “low” in this case, really mean 75 % keystone, 75 % of the energy in the most misaligned bands is coming from the pixel next to it. Note, that this is not the same scenario as one pixel containing two different objects, resulting in a linear mixture of two spectral signatures. With keystone in the data, some part of the spectral signature will come from one of the objects, while other parts of the spectra will have a 75% influence from the object next to it - giving an unphysical spectral signature. The keystone effect will effectively reduce the spatial resolution, as larger objects will be needed to get one pure pixel – one that is not influenced by the surrounding ones. This will obviously introduce effects like misidentification, misclassification and false alarms in this data product.
So, is low keystone distortion something that should only be expected in a scientific-grade camera? Is low keystone distortion only needed for high-end research, or is low keystone a requirement also in e.g. an industrial camera? Consider e.g. sorting of recycled glass. A major problem in the glass recycling business is that glass-ceramics (transparent and colored) are being put in the recycling containers for normal glass. When the recycled glass is melted, large glass-ceramic pieces (> 2mm) will not melt at the same temperature as the float (normal) glass, causing defects in the finished product. Such impurities could also destroy or damage the glass cutters and other equipment along the process.
To effectively remove the glass-ceramics that could potentially destroy a recycling batch, it is required to detect contamination pieces as small as 2 mm. Suppose a 1 m wide conveyor belt is being used to transport the cullet at 1 m/s. To stay above the Nyquist resolution limit a camera with a 1000fps speed or more is needed. Additionally, a camera with 1000 or more spatial pixels is needed to get two pixels per 2mm object in the across-track direction.
Using actual data, collected from a recycling facility, the spectra from 3 different glass-ceramics pieces will look e.g. like the samples selected below:
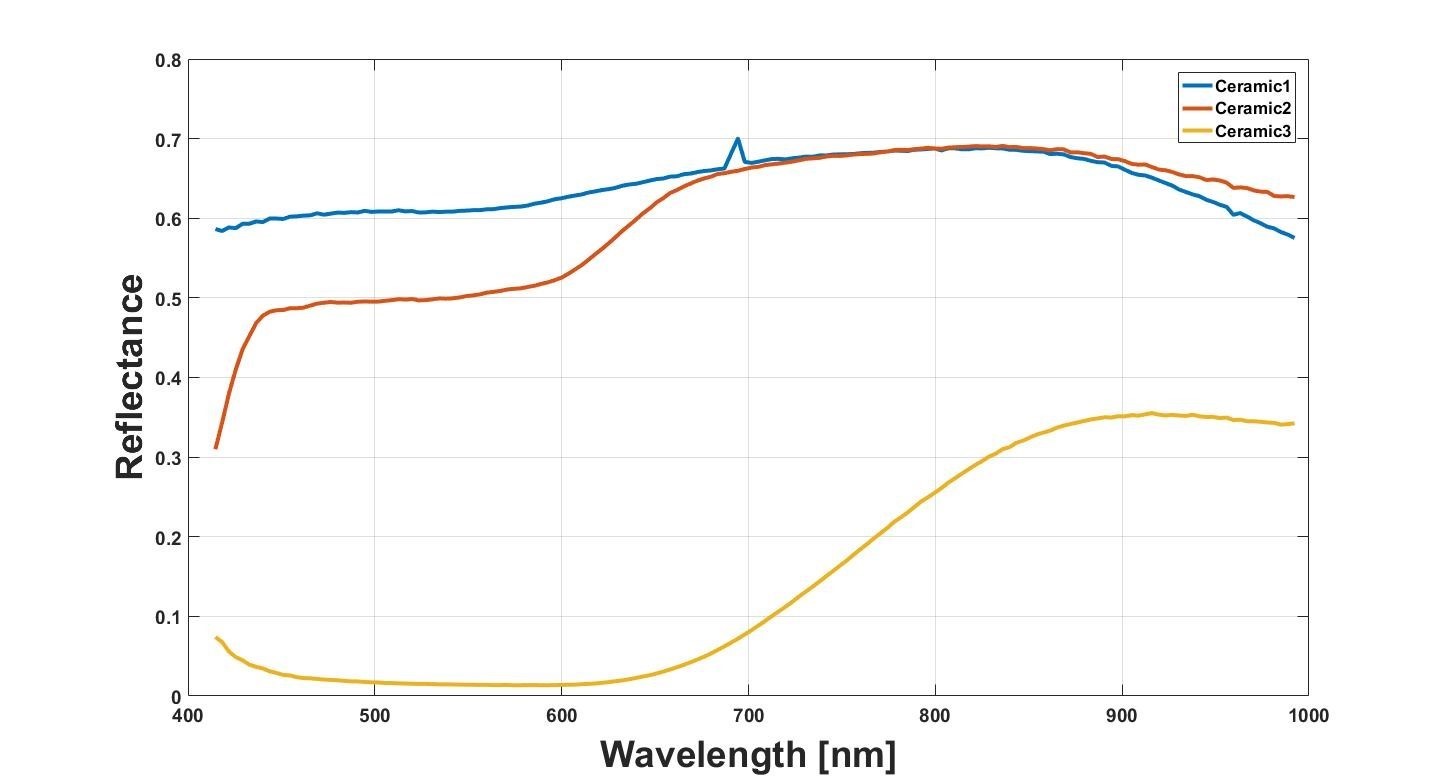
Actual spectra from 3 different glass-ceramics pieces.
Additionally, we have the spectra from 4 different recycled float glass types (green glass, brown glass, transparent – with weak blue component – and grey glass):
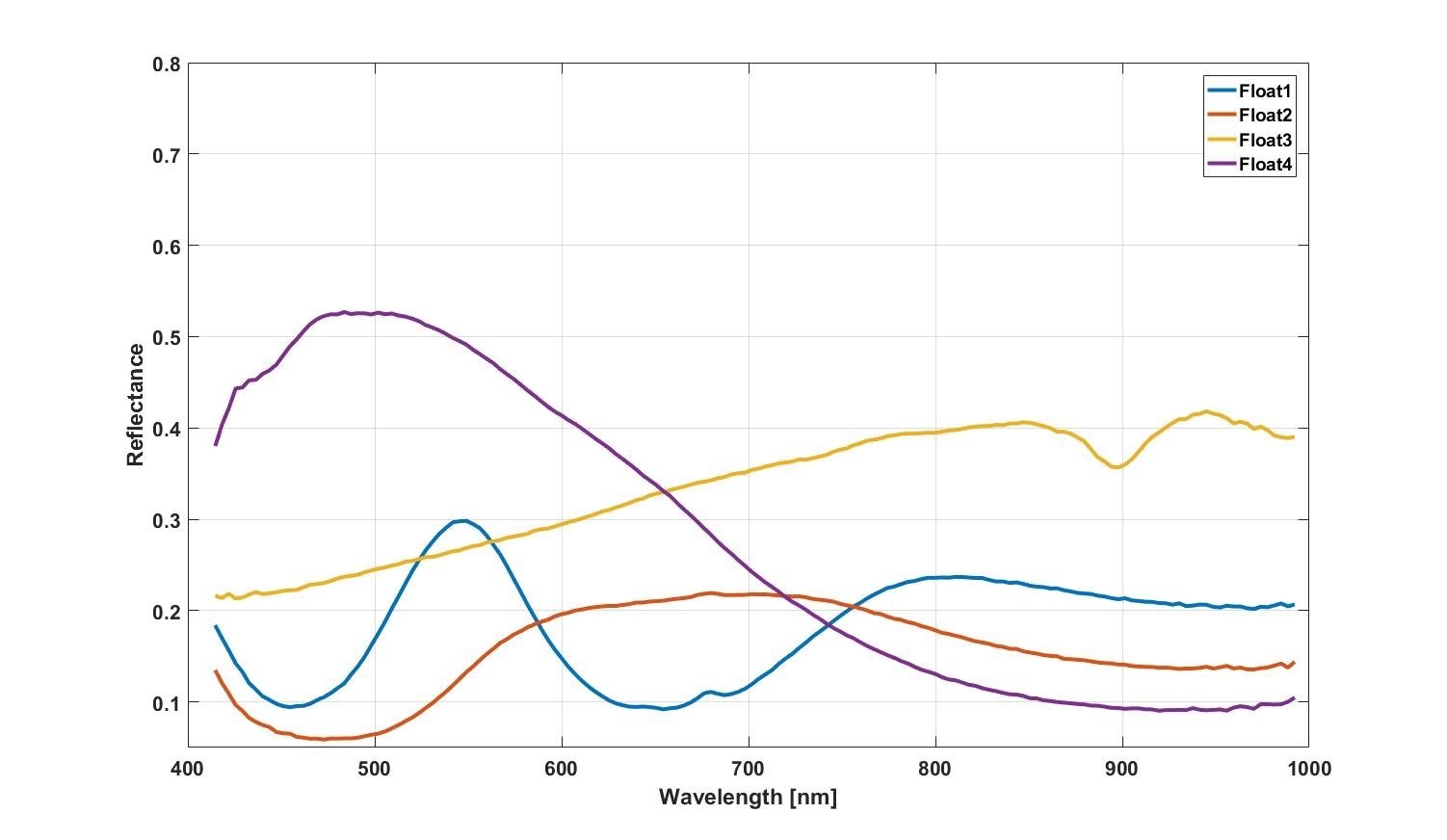
Four different recycled float glass types.
By creating an artificial scene with glass- ceramics samples that are 1, 2, 3 and 4 pixels large and all have the float glass spectra as background, the effect of keystone can be demonstrated:
Keystone in an infinitely sharp camera.
In this example, an infinitely sharp camera is being used - i.e. the PSF is not considered and the objects are perfectly centered on the pixel in both X and Y direction. In a real scene, these factors must obviously also be considered when selecting the correct pixel resolution for the camera.
Adding 10 %, 30 %, and 75 % keystone to the scene, the resulting RGB preview of the objects is shown in the figure below. Note that keystone has only been added in the horizontal directions, so there will be no distortions in the vertical direction.
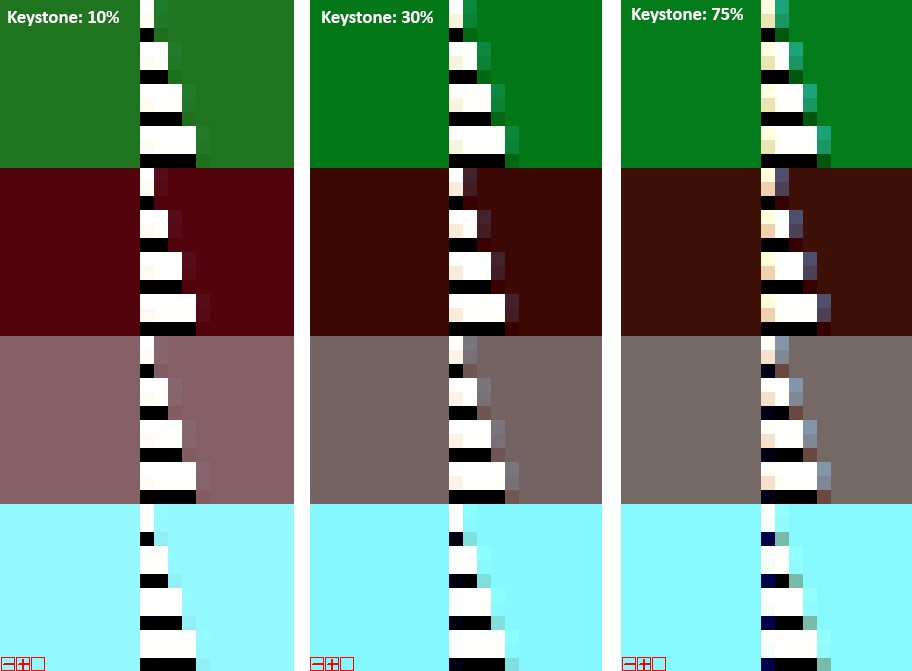
Demonstration of keystone.
As can be seen, the keystone is making some changes in the pixels that are visible in the RGB bands, but will it affect any classification results - e.g. a simple classification algorithm such as “Spectral Angle Mapper” (SAM)? This algorithm determines the multidimensional angle between two different spectra. The smaller the angle the more similar they are. With this algorithm, different threshold values can be set for the angles corresponding to the difference between the spectrum of the object to detect and the other objects that are in the scene. In this example, only the default angle in ENVI (0.1) is being used.
Running SAM on the original image, without keystone gives the following results:
SAM, infinitely sharp camera.
All the objects in the scene are detected unambiguously.
Repeating the exercise, attempting to detect the same objects in the data with 10%, 30% and 75% keystone, yields the following results:
SAM, cameras with keystone.
In this case, 10% of keystone does not change the results, even for the single-pixel objects. For a system with 30% keystone, the contribution of the effect is starting to be obvious. Looking in detail, with the Float1(yellow) background, all the Ceramic pieces are detected, but some of the border pixels are left unclassified (black pixels in the SAM image). For this application, where glass-ceramics is the detection target, that would not matter, but in other applications, Float1 could have been the target, and a one-pixel object would have been missed.
Looking at the Float2 background section (white background), it is noticeably more border pixels missing, but the glass-ceramic pieces are classified correctly. With Float3 as background (magenta), 30% keystone has no influence on the classified result. On the other hand, for Float4 as background (brown), the detection is starting to fail and the objects are no longer classified correctly. Note that this is with only 30% keystone. Furthermore, one pixel on the Ceramic3 is no longer classified correctly, and there are some wrong border pixels on Ceramic2 as well.
Continuing to the last case, with 75% keystone, the amount of classification errors has increased noticeably: Ceramic 2 classifies as Float3, Ceramic2 classifies as Ceramic1, Ceramic1 classifies as Ceramic2 and many of the glass-ceramic pixels are not belonging to any classification class. The worst case is Ceramic2 on Float2 background, where only one pixel on the 3-pixel object is classified correctly and 4 pixels are wrongly classified (in the object and at the borders).
From this simple example, it is evident that the keystone introduces huge errors in data that would result in a significant number of missed objects and many false alarms. As mentioned above, a camera with a large keystone value will effectively have reduced spatial resolution - meaning that higher resolution is needed to get one pure pixel if the keystone amount is the same per pixel.
As shown above, keystone will corrupt the results when the spectra that is to be detected in known. Since keystone is basically creating unphysical spectra, it will also corrupt other commonly used algorithms such as Anomaly Detection (CRX) and Principal Component Analysis (PCA).
With the latter, a benchmark is needed to assess how the PCA is corrupted by the keystone. Using a scene where there is a horizontal displacement of the object relative to the pixels, gives a linear mixture of two objects (spectra) without any unphysical spectra being generated (as mentioned above). To compare with the keystone effect, PCA bands 2,3 and 4 will be used to generate a false-color image for the image with objects being displaced 75% of a pixel and finally with the scene imaged with 75% keystone.
PCA classification.
Using this method, Ceramic1 and Ceramic2 cannot be easily distinguished where the scene is imaged with 75% keystone. Also, the background colors for float 1, 2, 3 and 4, has changed, indicating that the unphysical spectras have rotated the PCA into a new direction.
For the different hyperspectral camera technologies there are different origins of the keystone effect, making it important to understand the design of the sensor to be used – should reliable information on keystone values not be available. Also, it should be noted that essentially all instruments will be affected by keystone to some degree. Any misalignment between the bands will cause errors like those described above. As an example, an increasing number of commercially available systems are offered with a common slit combining the VNIR and the SWIR spectral range. The main argument for using a common slit is that both the VNIR and SWIR sensors are imaging the exact same spatial location at any given time. This allows for potentially very good co-registration between the VNIR and SWIR spectral ranges, if (and only if) the system is stable, both detectors are triggered with the same trigger and the same exposure time (integration time) is used. However, a common slit system with 75% keystone essentially eliminates all the arguments for having a common slit system in the first place, as there is already a 75% of a pixel misalignment between the bands. In this scenario, the data quality would be better if you use two separate instruments with low keystone (e.g. 10% of pixel size or better) and then make a precise geometric co-registration of the data. For airborne or UAV use, any dual-camera configuration (not with common slit) with an accurate boresight calibration and characterization (and with a reliable, high-precision navigation system) should be able to get better than 30% of a pixel co-registration between the VNIR and SWIR spectral range. Provided that each of the spectral ranges has e.g. 10% keystone, the system will perform significantly better than a common slit system with 75% keystone.
To conclude, misalignment between bands can have many different origins and the errors in the data caused by this effect are not negligible. When acquiring a hyperspectral camera, it is imperative to have sufficient information about the distortions affecting the system. A serious supplier of hyperspectral imaging systems will always deliver a test report with the hyperspectral camera where effects like spectral and spatial resolution, keystone and smile effect, straylight, SNR as a function of wavelength, NER and so on are measured and characterized on the actual camera that is supplied. Using only Nyquist as a reference when selecting a camera (selecting a camera with 2 pixels per the smallest object you want to detect) will only be a good idea if the camera have very low keystone (< 10% of a pixel). For cameras with e.g. 75% keystone, you should have at least 4 pixels per smallest object that is to be detected - but keep in mind that even with a pure pixel from a 4 pixel object, the keystone effect will also introduce a lot of false alarms, which must be acceptable for the operational scenario.
Finally, an important specification for any hyperspectral camera is its stability and repeatability. Suppliers offering systems with high keystone levels (e.g. 50% or more), cannot at the same time claim that the system provides great stability and repeatability. A system with a lot of keystone will essentially never be repeatable, as the behavior of a pixel will change depending on the spectrum of the object in the pixel next to it - thus making it very unrepeatable.
